Implicitly Defined Curves
Consider the equation \[6x + 3y = 2.\] We can solve this equation to get \(y\) explicitly as a function of \(x\)—namely, \(y = \frac{2}{3} – 2x\). On the other hand, the equation
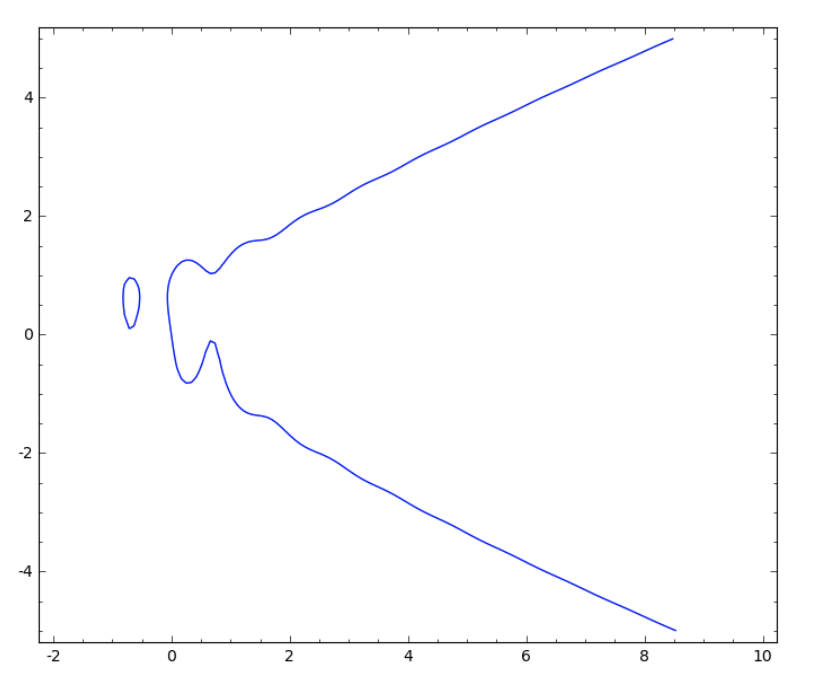
\[ y^4-y -\sin(2\pi x)= x^3+x \] cannot be solved for \(y\). Even though we cannot express the relation represented by this equation as an explicit function \(y = y(x) \), the equation still determines a curve in the plane:
This curve is made of points with coordinates \((x_0,y_0)\) which have the property that setting \(x = x_0\) and \(y = y_0\) in the equation gives a left- and right-hand sides which are, in fact, equal. For example, the curve contains the point \((x_0,y_0) = (0,1)\), since \[ 1^4-1-\sin(2 \pi *0) = 0^3 + 0. \] The curve displayed above is exactly the set of all such points \( (x_0, y_0) \), where \( -2 \le x_0 \le 10 \) and \( -5 \le y_0 \le 5 \).
1. Use the SageMath box below to determine which of the points given by your instructor lie on the curve given in your lab report. Record your answer on the lab report. (Recall the print() command which allows you to display multiple outputs at the same time and the N() command which produces a numerical approximation.)
2. For each of the equations given by your instructor, use the SageMath cell below to produce a plot of the implicit curve. (Replace the default equation, x - 2*y^2 == -3 with the one provided by your instructor. Recall from Lab 4 that SageMath uses the “double equal” sign “==” to represent the equality in an equation that we want to solve.) Then, either solve to express \(y\) as a function of \(x\) or explain why this cannot be done. If you can solve, then write \( y \) as a function of \( x \) in the second box of the SageMath cell below and in your lab report. If the equation cannot be solved for \( y \), explain in your lab report how the plot of the curve indicates that \( y \) is not a function of \( x \). In either case, attach a printout of your plot(s) to your lab report to justify your answer.